Optional Practical: Rolling cylinders (Algodoo)
Introduction
In this exercise you will investigate the motion of different cylinders rolling down an inclined plane using the simulation programme Algodoo. This is similar to the practical Rolling ball but since Agodoo is a 2D simulation you will be rolling disks down the slope instead of spheres. A disk has the same moment of inertia as a cylinder, mr2 for a hollow cylinder and ½mr2 for a solid one.
According to the law of conservation of energy the PE of the cylinder at the top of the ramp = Translational KE + Rotational KE at the bottom. So for a cylinder of mass, m rolling down a ramp of height h
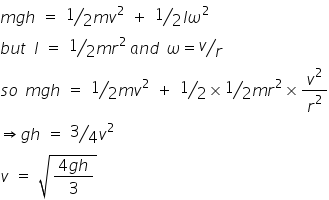
Making the ramp
You need to make a ramp of known height so it will be convenient to show the grid:
- Click the "turn grid on/off button".
- Double click to change settings, grid base 5 is a convenient scale.
- You want the window to be about 5m across, zoom in or out so you have the correct scale (you can see the scale at the bottom right of the window).
- Turn off air resistance by clicking the air resistance on/off button. When off the button is dark like this
 .
.

The ramp is made with the sketch tool  .
.
- Hold in the shift key then click where you want the ramp to start (1m above the ground).
- Drag out a line to the bottom of the slope and then release the shift button.
- Press shift again and draw the bottom of the ramp.
- Release the mouse key.
Rolling the cylinder
- Use the circle tool to make a cylinder of radius 0.2 m
- Place the cylinder at the top of the ramp.
- To measure the speed of the cylinder right click the cylinder and select plot. Choose time for the x axis and speed for the y.
- Click play to allow the cylinder to roll down the ramp.
- Determine the speed of the cylinder at the bottom of the ramp from your graph.
- Calculate the expected velocity using the equation above. Are they the same?
- If different try to work out why and adjust your simulation accordingly.
- Observe the forces acting on the cylinder by right clicking the cylinder then ticking "show forces" in the "appearance options". You may have to zoom in to see the friction.
Investigation
Use your simulation to answer the following questions
- The equation suggests that the velocity of the cylinder is independent of the mass and radius of the cylinder, is this true for the simulation?
- Does the angle of the slope change the final velocity?
- Try making a curved slope. Does this change the velocity?
- Derive an equation for the velocity of a hollow cylinder.
- To make a hollow cylinder draw a slightly smaller circle inside the one you have, right click the inner circle and select "subtract" from the "combine shapes" options. Delete the inner circle and you will be left with a ring.
- Roll the ring down the slope to find out if it has the velocity predicted.
- Experiment with some more complex rolling shapes like the one shown.

- Predict the effect of removing friction then use the simulation to see if you were right.
- Try rolling real cylinders down a slope. Use video analysis to measure the final velocity.
