Introduction

This is a brief description of how to construct a simulation of the Bernoulli equation in GeoGebra so you will need to be familiar with the basic features of GeoGebra. Although it looks complicated it's actually quite simple to set up, just takes time to put all the elements together. The Bernoulli equation is used to find the change in pressure as water flows through a pipe:

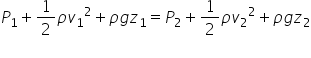
In this simulation the volume flow rate will be adjusted rather than the velocity so we will use the continuity equation to find the velocities.

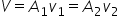
Setting up the sliders

As always the first task is to set up sliders for all the variable (there are many), it is important to set the ranges so that the values will make some practical sense. Problems often involve water in pipes so pipe diameters are a few cm, height differences a few m density is 1000 kgm^-3, flow rates are cm³ s^-1 (or l s^-1 ) and pressures in kPa. For calculations it is important to use SI units so we will have to convert the units in the calculations

• z₁ from 0 to 10 increment 0.1 (to get the subscript type z_1).
• z₂ from 0 to 10 increment 0.1
• P₁ from 0 to 1000 increment 0.1
• P₂ from 0 to 1000 increment 0.1
• ρ from 0 to 5000 increment 100
• r₁ from 0 to 5 increment 0.1
• r₂ from 0 to 5 increment 0.1
• Arrange the sliders so the 1's are on the left and the 2's on the right.
• Fix the slider lengths to 100 px (this can be done in one go if you highlight all of them)
• Fix the position of the sliders as absolute.

Calculating velocities and Pressure

Before making the simulation you need to do some calculations first the velocities

• Use the continuity equation to calculate the velocity v₁ and v₂ (remember to convert cm to m in your calculation).
• Display the velocities under the sliders by making a text box (include units).

Then the pressures. You first need to set the incoming pressure P₁ , this is created by a head of water or pump.

• Make a slider for P₁ from 0 to 1000 increment 0.1 (this is kPa).
• Use Bernoulli equation to calculate P₂ (be careful with the units here, you want the answer in kPa but your calculation must be in SI).
• Display P₂ using a text box.

The sliders are all numbers but it would be better if they had units.

• Create a text box for each slider value including units.
• hide the slider label.
• move the text box label to the slider an fix its position.

Adding graphics

You could leave your simulation as a simple calculator but you will get much better idea of how the quantities are related by adding an animation.

• Using the "move graphics view tool", shrink the x axis so that it extends from -30 to +30 leaving y so it goes from 0 to 10

This is so that the circles used to mark the end of the pipe appear as ellipses.

• Add line y = z₁
• Add line y = z₁ + r ( this marks the top of the pipe)
• Add line y = z₂ - r (the bottom)
• At about x = -10 add a circle with centre on y = z₁ and radius r (this will be an ellipse due to scaling)
• Add points where the circle intercepts the pipe and where the outside edges of the pipe intercept the y axis.

• Hide the 3 lines and add segments to mark the edges of the pipe.
• Hide all points and labels.

Now you use the same idea to build a pipe on the right side extending from x = 10 to x = 20. Join this section to the other with line segments. If you want to finish it properly then you can:

• Fill with colour by drawing a polygon the between all the edge points.
• Add velocity vectors by using the "line segment with given length tool" then adding a vector to give the arrow.
• Add manometers to show pressure also using the "line segment with given length tool" and playing with the edges to make the manometer tube go up and down with the pipe (you can work that out for yourself).

Note that in my simulation the radius of the pipes and the height difference are not to scale nor are the manometers (this is to get them all to fit in the picture)
radius - cm
Height - m
Manometer - 100m (so you must multiply your simulation length by 100 to convert to m)