Activity: Angular momentum

Short and sweet. You'll learn how to define angular momentum and then how to apply conservation of angular momentum.
The angular momentum of a point mass, m moving in a circle of radius r at speed v is given by:
Angular momentum = mvr = mr2ω
For a rigid body with moment of inertia, I spinning with angular velocity ω:
Angular momentum = Iω
According to Newton's second law:
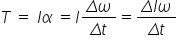
So if there are no external torques acting (T = 0) then there is no change in angular momentum which means that it is conserved.
In the following animation the two spinning balls are pulled together by shortening the spring joining them.
- Explain why they rotate faster when the spring gets shorter.
The next one shows a car in space. Watch what happens as the motor starts to make the front wheels rotate.
- Why does the whole car start to rotate?
- Why doesn't the centre move?
Here is a real example:
- Explain why the ice skater spins fastest at when her leg is up straight.
A clip from One Minute Physics with a more sophisticated version of angular momentum:
You can experiment with Algodoo yourself, here are some instructions Conservation of angular momentum (Algodoo).
Using the PASCO apparatus in the photo, find out if angular momentum is conserved when a lump of Plasticine is dropped onto the spinning beam.

Use what you have learnt to explain how some of the following spins work:
and some more...
- There are some problems to solve in the book (exercises 25 to 28).
- Angular momentum multiple choice quiz
