Applications HL Scheme of Work
 The new HL syllabus covers 240 hours of lessons (including the 30 hours of "mathematical toolkit"). There is a lot of new material in the applications course - how much is new will depend, at least to some degree, which HL "options" (calculus, stats and probability, discrete etc.) teachers have experience of teaching as the majority of 'new' items come from various pre-2019 syllabus HL "options".
The new HL syllabus covers 240 hours of lessons (including the 30 hours of "mathematical toolkit"). There is a lot of new material in the applications course - how much is new will depend, at least to some degree, which HL "options" (calculus, stats and probability, discrete etc.) teachers have experience of teaching as the majority of 'new' items come from various pre-2019 syllabus HL "options".
A reminder that on these pages there are a set of posters, giving an overview for students, parents and colleagues, of the entire content for SL and HL in both the Applications and interpretation subject and Analysis and approaches, as well as the common content
The below important information impacts on the development of a Scheme of Work. However, if you are in a hurry to dive into a week-by-week content guideline, click here.
Applications and Interpretation focused
The design and elements of the course actually allow for a good deal of creativity in designing a course. There are a wide range of useful schemes of work that teachers can vary according to . .
- What order is necessary? What can change?
- When will I do the Internal Assessment? What has to come first?
- If you also have to teach IB students: AP statistics, AP calculus, the German Arbitur, A-levels, Chinese GaoKao, All India Secondary school leaving Certificate etc. - this will obviously impact the order, and time, spent on different topics.
- Which cross unit topics might go well together? Where do concepts overlap?
The scheme outline
The first unit (seven weeks of four hours/week of lessons + 1 hour end of unit test) is planned out week by week with lesson by lesson suggestions and resources. For units 2 to 6 outlines only (currently) are provided. These will be developed into schemes similar to unit 1, with links to resources (where available) ahead of September. As the materials develop on the new website it will become a fully resourced scheme of work.
Added to the total number of hours shown below should be 6 hours of end of unit tests (1h per unit test), the average of which I use as my predicted grade for students (see above) and 1h for various short quizzes.
The topics in each unit are colour coded as per the below key to show the link between the new applications and interpretation topics and the previous IB 2012-19 syllabi :

1.Financial Mathematics & Introduction to Modelling Techniques - 30 hours
2.Statistics and distributions - 44 hours

3.Modelling with functions - 46 hour

4.Measuring Change - 32 Hours

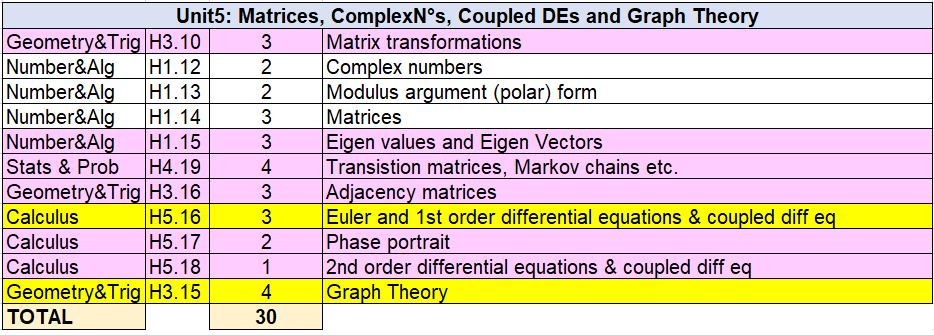
5.Matrices, Complex numbers, and Graph Theory - 30 hours
6.Geometry (including Volumes of revolution & voronoi diagrams) - 39 hours
.png)
The Internal Assessment - 12 Hours
Assessments and review - The guide does not obviously take in to account the need for periods of assessment and review. This scheme of work aims to build these in to the 240 hours. Some schools may get more time than this which allows for greater flexibility, but many don't.
Weaving into your Scheme of work the IB Approaches to Teaching and Learning, the Mathematics Toolkit, Internal Assessment, Paper 3 practice, Tok, CAS and Extended Essay (the whole supported by/aiming to develop, the IB learner profile).
It was always the intention that the internal assessment be an organic evolution/extension of the investigative, concept-based classroom experience of IB students. The 30 hours allocated to the mathematics toolkit (see p.18 of the Guide), 10-15 of which are recommended for the internal assessment (see p.82 fo the Guide), is designed to provide more time for teachers to embed these ATLs in IB students regular day-to-day.
Whilst the above may seem daunting when expressed as a list, isolated from content, once understood as the means through which content is delivered (takes form), it becomes integrated in our pedagogy and in support of, and served by, the delivery of the content.
Cross-Unit Links
One of the aims of a concept focused, inquiry approach to learning is to make explicit the connections across seemingly different areas of mathematics.
(A) Use of eigen values (at HL) threads together seemingly (on the surface) disparate topics:
- Vectors
- Matrices
- differential equations
(B) Solving simultaneous equations threads through:
- S1.8 systems of linear equations in up to 3 variables
- H1.15 representing 2x2 polynomials using matrices (and solve)
- S2.4 finding the intersection of two graphs.
- H3.12 Finding positions, intersections . . . times and distances when two objects are closest to each other.
(C) Trigonometric Functions thread through:
- H1.13 polar form of complex numbers and adding sinusoidal functions
- S2.5 asinbx & acos(bx)+d, H2.9 sinusoidal models.
- S3.3 Applications of right and non-right angled trigonometry
- H3.8 Graphical methods of solving trigonometric equations in a finite interval
(D) Maximums and Minimums of functions using the derivative thread through:
- H3.12 finding times and distances when two objects are closest to each other
- S5.7 Optimisation problems in context.
(E) Derivative as a rate of change (kinematics) threads through:
- H5.10 Use of second derivative test to distinguish between a maximum and a minimum point.
- H5.13 Kinematics involving, displacement, velocity and acceleration
- H3.12 Vector applications to Kinematics
...
This 'subject': Applications and interpretation (with either the HL or SL 'course') is new, with a new name and a new structure. The next curriculum review is likely just to be fine tuning. That means that we will have at least 14/15 years of this course (and probably more). What I find most stimulating about the new subject is the central aim to make the applications explicit. Our young people are growing up in what is widely held to be 'the 3rd industrial revolution' (now the '4th industrial revoluiton!'). Mathematics lies at the heart of this exciting evolution in technology, Fusion energy, drone development, crypto currencies etc. etc. Trawling through the history of mathematics, one finds an interplay, a 'feeding of the one from the other', between pure and applied mathematics. I think it is rare (if at all) that mathematicians responsible for the development of a new area of mathematics were not aware, and their work influenced, by the scientific/technological problems of their day. To this end, the following scheme of work is designed around solving, and developing, solution(s) to a central 'problem' i.e. putting the learning of mathematics into/against the context of solving a concrete problem. As Elon Musk has commented when interviewed about the school he has provided for his own children: "it's important to teach to the problem, not to the tools . . a more traditional course would start with teaching you all about screwdrivers and wrenches . . a better way to do it would be to say, "here's an engine, now how are we going to take it apart?". Oh, we'll need a screwdriver, that's what the screwdriver is for, we'll need a wrench, that's what the wrench is for . . this way a very important thing happens, the relevance of that tool becomes apparent".
SL as a subset of HL
In an HL/SL mixed classroom, the spread of abilities will be large. A pilot by the IB on 2012-2019 syllabus HL/SL students suggested that HL students complete questions on average about 30% faster than SL students. This time saving, taken into consideration alongside the greater depth of understanding that is required of an HL student e.g. an HL student’s deeper understanding of the concepts around “t-tests” – unbiased estimators of population standard deviation from a sample, central limit theorem (items not included in the SL syllabus) etc. means not only a different speed, but perhaps a different approach also.
A class of SL Level 5 and above, mixed with an HL class, is likely to be a better combination than an unfiltered SL/HL mix (depending on the numbers and flexibility of staffing/timetabling in any particular school). Teaching classes from SL level 3 (or below) to HL level 7 would be challenging.
University Entrance Requirements
As the new subject's: Applications and interpretation, HL course starts September 2019 university's are, in ever-increasing numbers (exponentially?), declaring which of their degree programmes will accept HL Applications and interpretation.
There is a lot of variation in the announcements being made by Universities concerning which university degree programmes will require what subject. It is important that each school/IB institution contacts the universities their current students/past students have typically applied to to find out what their different courses require. To help give you an idea of what to expect, further below is a selection of replies from a range of North American and European countries. Please do share any official responses you have received from universities in the comments section at the end of this page i.e. asian, australasian, south american, african universities
McGill, Canada announced early on: "For our programs which have maths as a prerequisite requirement, we will accept HL & SL Analysis and HL Applications".
Western Washington University (USA)
WWU will give credit for scores of 4 and higher on HLs and most SL courses.
https://admissions.wwu.edu/international/ap-ib-and-cambridge-international-credit
Warwick University, United Kingdom announced early on what I think sounds like an accurate assessment of the differences between the HL Applications and interpretation and HL Analysis and approaches subjects:
"Analysis and Approaches is required for Mathematics (although note that Applications and Interpretation is sufficient for the joint BSc Mathematics and Philosophy degree), Physics (including BSc Mathematics and Physics), Computer Science
Applications and Interpretation is acceptable for Chemistry, Economics, Engineering, Life Sciences, PPE. It is further accepted by Statistics on the basis of a higher grade result. BSc Accounting and Finance – awaiting confirmation from the department.
GERMAN Universities
Either HL required for STEM programs.
Any of the 4 mathematics (SL and HL) courses for NON-STEM programs: https://www.ibo.org/contentassets/1b11a2a3337345228cf611e04f5b4758/faq-german-recognition-eng-.pdf
SWISS Universities
All of them accept A&I and A&A as equivalent. EPFL (Lausanne) and ETHZ (Zurich) require HL in either strand, all the other universities accept SL in either strand.

