Practical: Measuring half life of beer foam
Introduction
This practical is adapted from a worksheet posted by Mark Headlee (UWC USA) on the OCC.
When you pour a glass of beer the gas in the beer forms bubbles (called a head), when you are going to drink the beer you try to minimise this effect but in this experiment you will make it as much as possible by pouring fast and using warm beer. The bubbles burst randomly so rather like the decay of radioactive nuclei the rate of decay of bubbles is proportional to the number of bubbles so:
dN/dt=-λN
Solving this differential equation gives
N=Noe-λt
Where
No is the original number of bubbles
N is the number of bubbles at time t
λ is the decay constant
It’s not possible to count the number of bubbles but you can measure the level of beer which increases as the bubbles burst. This will give you an exponential increase however if you measure the height of the beer downwards from the final level (when there is no foam) then you get an exponential decay that is proportional to the decay of the foam.
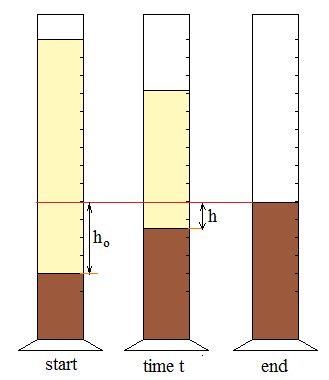
Now
h=hoe-λt
Where ho is the original height of the beer measured downwards from the final height.
Method 1.
You are going to pour the beer into a measuring cylinder but before you do this tape a strip of paper to the side of it; this will be used to mark the beer level. You will also need a stop clock; either use your mobile phone or an internet clock.
Shake up the beer and pour it quickly into the cylinder, as soon as it settles a bit mark the beer level on the tape, do this every 5 seconds. If you are well organised up to 3 people can mark the same cylinder.
Continue marking for 2 minutes then let the beer stand for a further 3 minutes. There will still be some foam in the flask but you are going to ignore this and assume all the bubbles have burst, mark this on the tape, this will be you zero.
- Take the tape off the cylinder and lay it flat ready for measuring with a ruler.
- Measure from the end point to the measured levels entering your results into an appropriate table.
- Plot a graph of height vs time and use it to find the half life of the beer foam.
If 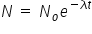
then 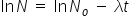
This means that a graph of lnN vs t will be a straight line with gradient -λ.
Use a spreadsheet to find lnN and plot a graph of lnN vs t to find a value of λ and hence the half life of the foam.
Method 2.
In this method Loggerpro will be used to analyse a video of the beer rising up the glass.
- Open LoggerPro and choose video capture from the insert menu. Arrange your webcam so that you can see the measuring cylinder on the table. If this doesn't work then it might be because you don't have "Quicktime" installed on your computer.
- When ready pour the beer and video it for 5 minutes. Units are not important but if you want to you can put a ruler next to the cylinder so that you can calibrate the video.
- Go to the end of the video and set the top of the beer as zero using the set origin tool.

- Now rewind to the beginning of the video and start marking the level of the beer as it rises up the cylinder. You probably won't be able to see any difference from one frame to the next so advance in steps that are big enough to see some movement.
- When you are finished marking the points you should be able to see an upside down decay curve. You can make it positive by creating a calculated column where the y values are multiplied by -1.
- Fit an exponential decay curve to your data and find the decay constant.
