Optional Practical: Iterative SHM (Excel)
Introduction
When a body executes SHM its acceleration is proportional to its displacement from a fixed point and always directed towards that point, this obviously means that the acceleration is not constant however if we consider very small steps then we can assume that the acceleration is constant for the duration of the step and can therefore use the familiar suvat equations to model the motion.
Setting up the spreadsheet
- Make headers for time, displacement, velocity and acceleration
- Make a small table for the variables amplitude, constant and time interval
- Set values as shown below. Notice k is -ve since the a is proportional to -x.
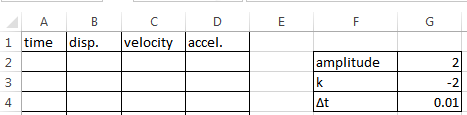
- The time starts from 0 and increases by Δt each step so enter 0 in the first cell and =A2+G$4 in the second. Drag this equation down for about 500 cells.
- The oscillation will start at the maximum value so the initial displacement = amplitude so enter =G$2 in the first displacement cell.
- Initial velocity is zero so enter 0 in the first velocity cell
- Acceleration is proportional to displacement, the constant of proportionality here is k, so enter = G$3*B2 in the first acceleration cell.
Here comes the tricky bit:
We can use s = ut + 1/2at2 to calculate how far the body will move in time Δt, this can then be added to the previous displacement to find the displacement from the fixed position.
- Enter the equation =B2+(C2*G$4+0.5*D2*G$4^2) in the second displacement cell.
- To calculate the final velocity (which will be initial velocity for the second step) we will use v = u + at so enter =C2+D2*G$4 in the second velocity cell.
- The new acceleration will be calculated from the new displacement you can simply drag the first equation into the second cell.
- Highlight the equations in row 3 and drag them to fill the whole table.
To plot a displacement time graph simply highlight the first two columns and insert > chart > scatter

- Try changing the values of amplitude, k and Δt to see what happens.
- The equation for SHM is a = -ω2x, Show that k = ω2 (remember that ω = 2π/T )
- As time progresses the amplitude increases, why is this?
- If the time increment is large the amplitude increases a lot, why is the model so bad with large Δt?
- Plot displacement, velocity and acceleration vs time on the same graph. Observe the difference in phase between these quantities.
