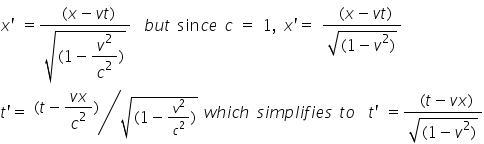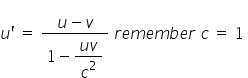Activity: Spacetime diagrams

Time for a bit more interaction. Today you will construct an interactive space-time diagram using GeoGebra and, as a result, understand how space-time diagrams can be used to represent events in two frames of reference.
 I should first clearly acknowledge the work of Kristian Evensen who created Interactive Minowski which gave the inspiration for this worksheet and was a great help when making diagrams for my text book.
I should first clearly acknowledge the work of Kristian Evensen who created Interactive Minowski which gave the inspiration for this worksheet and was a great help when making diagrams for my text book.
This isn't for the GeoGebra beginner but if you know the basics then you should be able to follow the instructions. Space- time diagrams are used to represent the transformation of space and time between two frames of reference. The way this is achieved is by inclining the time and distance axis.
The first thing to realise is that in a space time diagram time is represented on the y axis. To make things simple time will be represented in units of 1 s and distance in light seconds this will make the gradient of a body travelling at the speed of light =1 (You could also use time in years and distance in light years)

So for the graph above the velocity of light = 1/gradient = distant travelled by light in 1 second /1 second. A body travelling at less than c will have a gradient greater then 1 (remember time is the y axis).
Note that because of the units v will be expressed in terms of c so if gradient 1, velocity = c. If gradient = 2, velocity = 0.5c
- Open a new GeoGebra file.
- Add labels to the axis. (right click workspace>graphics>axis)
- Add the line y = x (type y = x in the input line at the bottom of the window)
- Change colour of line to red (Right click line and choose properties)
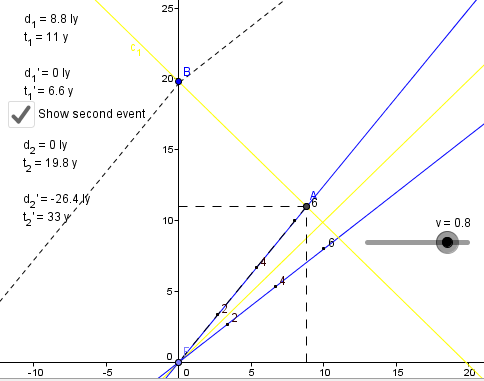
Two events that take place at the same position according to the girls can be represented by points on a line parallel to the t axis. If F is one event then a second event at the same place according to the girl will be represented by a point on the t axis.
- Place point A at the 4s mark on the t axis.
- What is the time between events F and A according to the girl
- What is the time between the events for the car?
- Check you answer using the time dilation formula.
t' = 4.36 s
- Make an event that happens at the same place as F but 4s later with respect to the car.
- How long after event F did this take place according to the girl?

- Lock the x and y axis so they always have the same scale by right clicking on a blank area of the graph and from graphics > preferences > basic set x:y to 1:1 and lock by clicking the padlock.
- Add a line segment (m) from the origin to the point representing t' and hide it.
- Add a circle with centre (0,0) and radius 2m/t' (if 2m is the distance from the origin to point representing t' then 2m/t' will be 2 units long).
- Add points were the circle intersects t' and x' axis.
- Make the points small and black.
- Hide the circle and all labels.
- Repeat for the 4 and 6 markers (you can add unit markers if you like).
- To display the numbers open point properties enter the relevant number as the caption tick "show label" and change to caption.
- Now you have scales it might be neater to remove the floating values and place them somewhere else.
- To add a t' x' grid to the graph you can add lines parallel to x' and t' that intersect with the scale points.
Alternatively a neater version suggested by Maciej Pietka is to use the sequence function and the equation of the lines that mark the grid lines. To explain this requires the use of the reverse transformation but you can simply copy the code:
- Sequence[ y = v x + i sqrt (1- v^2), i, -5, 5 ]
- Sequence[ y = (x - i sqrt (1- v^2)) / v, i, -5, 5 ]
I don't like adding details without explanation so here is my attempt to explain the equations for the d' grid lines (t' have a similar explanation):
The grid lines are parallel to d' so have the equation y = vx + k where k is the y intercept. To plot these lines we need to know the intercept so lets take a point that we know is on the line and use the equation to find the value of k. Let's consider the convenient point below.

Lines on the graph are all plotted with respect to the original x and y axis (d and t) so we need to know the coordinates of this point in the girls frame of reference. We can see that d' = 1 l s and t' = 1 ls but what do d and t equal?
Here we have to use the reverse transformations

What the sequence function does is plot one of these lines for every second in t'.
The equation for the time lines can be derived in a similar way but maybe that's enough maths for now.
Here is the clean version (to save time you could use this):