Activity: Acceleration and suvat

Here you will define acceleration and come to understand its vector nature. You will learn how to calculate acceleration when it is constant and determine it using the gradient of a velocity vs. time graph. The 'suvat' equations of uniformly accelerated motion are derived and problems of constant acceleration are presented for you to solve.
Need to know
Acceleration is defined as the rate of change of velocity, so if velocity changes there must be acceleration.
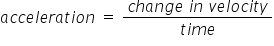
- If a car drives round a corner it must be accelerating even if the speed is constant, why?
- In this part of the course we are only interested in constant acceleration. This means the motion must be in a straight line, why?
.png)
So far we have two equations that define this motion
From the definition of acceleration: 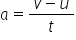 (1)
(1)
and average velocity: 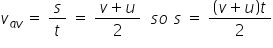 (2)
(2)
It might seem strange that the average is found by adding the max + min and dividing by 2 but this works because the acceleration is constant like the heights of the following students.

Use these equations to solve the exercise on page 43.
So far you have been measuring simulated motion with constant acceleration. For the next four classes you will be considering real motion.
Now know
For subscribers to StudyIB
 suvat problem 3
suvat problem 3 suvat problem 4
suvat problem 4
 This activity mainly uses simulations, however students will need to measure the acceleration due to gravity in real life.
This activity mainly uses simulations, however students will need to measure the acceleration due to gravity in real life. 




 suvat problem 1
suvat problem 1 suvat problem 2
suvat problem 2 suvat problem 5
suvat problem 5