Interactive textbook: Measurement and uncertainty
What is physics?
Physics is  all about deriving relationships between quantities so that we are able to make predictions. To derive relationships, we need to be able to measure the size of the quantities.
all about deriving relationships between quantities so that we are able to make predictions. To derive relationships, we need to be able to measure the size of the quantities.
An example of a quantity: Density
A large ball of plasticine is heavier than a small one. To quantify the size we can measure the volume and to determine how heavy the ball is, we measure mass. If we did this for lots of different plasticine balls, we would find that the ratio of mass to volume is always the same:
Mass is proportional to volume.
\(m \propto V\)
\(m=kV\)
...where k is the constant of proportionality
The mass of a bag of identical apples is proportional to the number of apples.
What is the constant of proportionality?
Mass of apples = mass of one apple x number of apples
 The constant of proportionality is called density, \(\rho\). If we know the density of a substance we can calculate its mass from its volume:
The constant of proportionality is called density, \(\rho\). If we know the density of a substance we can calculate its mass from its volume:
\(m = ρV\)
If we plot a graph of mass against volume we get a straight line:

This line has the general equation \(y = Ax\) where \(A\) is the gradient \(Δy\over Δx\).
Let's compare the two equations:
\(m = ρV\)
\(y = Ax\)
If \(m\) is equivalent to \(y\) and \(V\) is equivalent to \(x\), then \(ρ\) is the gradient. In the example represented by the graph, \(ρ = 1000 \text{ kg m}^{-3}\) (which happens to be the density of water).
The graph represents of the mass of different bags of apples vs the number of apples.
.png)
What does the gradient represent?
Mass of apples = mass of one apple x number of apples
gradient = mass of apples/number of apples = mass of an apple
Quantities and units
In physics, numbers represent quantities. To show what quantity is being represented we use units, such as \(1000\text{ kg}\) or \(2\text{ m}^3\). These are not the only units of mass and volume but are also SI units. Whenever a new quantity is introduced in this textbook, make sure you note its SI units.
 You don't have to use SI units, but most derived units depend on it. When using the equation \(F = ma \), the force is only in Newtons if \(m\) is in \(\text{kg}\) and \(a\) is in \(\text{m s}^{-2}\).
You don't have to use SI units, but most derived units depend on it. When using the equation \(F = ma \), the force is only in Newtons if \(m\) is in \(\text{kg}\) and \(a\) is in \(\text{m s}^{-2}\).
In some cases, non-SI units will cancel. When calculating \(v\) from \(v = {m_1\over m_2} u\), the masses \(m_1\) and \(m_2\) can be in any units provided the same unit is used for both.
So far we have mentioned four quantities: mass, length, volume and density. Mass and length can not be broken down into anything smaller so are termed fundamental quantities![]() . Volume is length x length x length and density is mass/volume; these are derived quantities
. Volume is length x length x length and density is mass/volume; these are derived quantities![]() .
.
Speed is defined as the distance travelled per unit time.
What are the SI units of speed?
m s-1 is the same as m/s
Uncertainties
You can never measure a quantity exactly. There will always be an uncertainty and it is important to quote the uncertainty with the value, e.g. \(12.00 ± 0.01\text{ m}\).
 If \(L\) represents length and \(ΔL\) represents its uncertainty, a physicist would note their result as \(L ± ΔL\).
If \(L\) represents length and \(ΔL\) represents its uncertainty, a physicist would note their result as \(L ± ΔL\).
The fractional uncertainty is \(ΔL\over L\).
The % uncertainty is \({ΔL\over L} \times 100 \%\).
This means that the length could be anything from \(11.99\text{ m}\) to \(12.01\text{ m}\). Note:
- The uncertainty is quoted to 1 significant figure.
- The value of the quantity cannot be quoted to more or less decimal places than the uncertainty.
Uncertainties can be due to the instrument itself. The stop clock on an iPhone gives a time to \(0.01\text{ s}\) so the measurement uncertainty is \(± 0.01\text{ s}\).
The mass and diameter of an apple are measured as shown.

What are the uncertainties in mass and diameter?
For a digital scale the uncertainty is about ± the smallest digit.
Measuring the apple with the ruler positioned as shown is very inaccurate.
However, sometimes uncertainty is higher than the measurement uncertainty, depending on how the instrument is used. Imagine that 21 people measured the time taken for a runner to cross the finish line in a 100 m race and recorded their times by putting a dot on a paper chart:

Some measurements were too long and some too short, but most of the times recorded are around the middle of the range. The mean value is \(12.7\text{ s}\). We can take this to be close to the actual time. The longest time is \(14\text{ s}\) and the shortest about \(12\text{ s}\) so the uncertainty (half the range) is \(±1\text{ s}\). The final result is therefore:
\(13 ± 1\text{ s}\)
Note that the number of significant figures in the time was reduced from \(12.7\text{ s}\) to \(13\text{ s}\) due to the large uncertainty.
 The 'half the range' method does not always reflect reality. If more measurements are taken the mean becomes more accurate but the range becomes bigger. The latter effect increases the uncertainty.
The 'half the range' method does not always reflect reality. If more measurements are taken the mean becomes more accurate but the range becomes bigger. The latter effect increases the uncertainty.
The variation of results for the same measurement is caused by random error but there might also be a systematic error. If all the clocks were started automatically by the sound of the starting gun but the sound took \(0.4\text{ s}\) to reach them, all the clocks would start late and record times that were \(0.4\text{ s}\) too short. This is called a systematic error and would mean the data would be recorded as follows:

The table shows the mass of different numbers of apples.

According to our theory the mass of apples should be proportional to the number of apples but it isn't. What is this due to?
All measurements are 0.002 g too big, this is probably due to the mass of the bag. A systematic error
Estimating uncertainties
There are two ways to estimate the uncertainties associated with in experimental data:
- The measurement uncertainty is estimated based on the resolution of the measuring device (half the smallest division for analogue scales e.g. rulers and equal to the smallest division for digital scales e.g. balance)
- Repeated measurements are taken to calculate the error from the spread of data (half the range)
The largest of these is the uncertainty used.
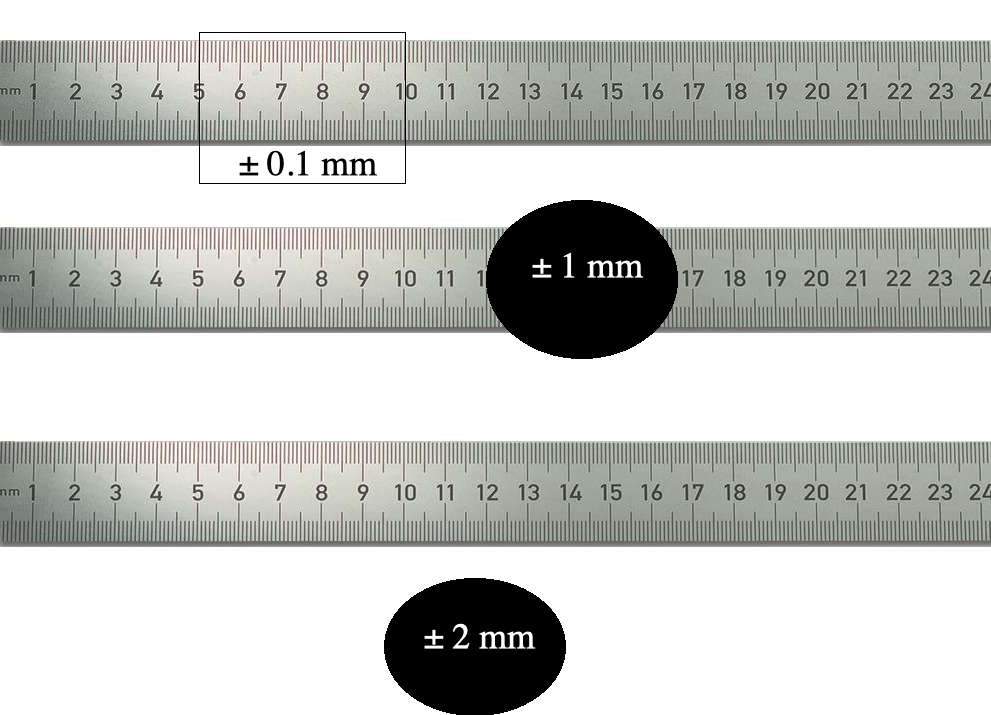
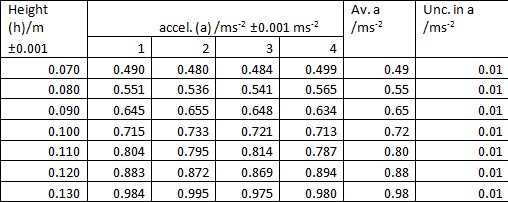
The estimated measurement uncertainty is recorded in the header of the results table because this will be equal for all data in the column. A calculated uncertainty needs a column of its own because of the variation associated with repeats or in converting from fractional to absolute uncertainty. In the example below you can see the estimated uncertainty in acceleration is much less than the calculated uncertainty:
Propagating uncertainties
When quantities are calculated, we must also calculate the new uncertainty. For example, if we calculate the volume of a sphere using a radius value of \(2.0 ± 0.1\text{ m}\) then we could calculate the maximum and minimum values and find the uncertainty:
\(V = {4\over 3} πr^3 = 33.51\text{ m}^3\)
\(V_\text{min} = 28.73\text{ m}^3\)
\(V_\text{max} = 38.79\text{ m}^3\)
\(ΔV = ± 5\text{ m}^3\)
\(\Rightarrow V = 33 ± 5\text{ m}^3\)
An alternative method uses the fact that the fractional uncertainty is added when values are multiplied but not changed when multiplied by a constant.
\({ΔV\over V} = {ΔL\over L} + {ΔL\over L} + {ΔL\over L} = 3{ΔL\over L}\)
\({ΔV\over V} = 3 \times {0.1\over 2} = 0.15\)
\(ΔV = 0.15 \times 33.5 = ± 5\text{ m}^3\)
If values are added or subtracted, the absolute uncertainties are added.
If values are multiplied or divided, the fractional uncertainties are added.
A box is filled with apples counted as they travel quickly along a conveyor belt, this leads to an uncertainty 0f ±2 in the number of apples.
If the mass of the box of apples = 15.4 kg and the number of apples = 75
What is the % uncertainty in the mass of an apple
mass is measured to ± 0.1 kg so the % uncertainty = 0.6%
The % uncertainty in number = 2.7%
So the % uncertainty in mass/number =3.3%
Graphing data
When plotting experimental data there are two options:
- Plot the unprocessed data and fit a curve
- Process the data in such a way that, when plotted, a straight line can be fitted
The former approach with the curve shows the general shape of the function but is more difficult to interpret; curves should only be fitted to data if the function is known.The latter approach is called linearising. The advantage of linearising is that the gradient and intercept can be calculated, both of which will have their own real-world meaning.
Taking the example of measuring different sized solid spheres, if the radius and mass were measured the relationship is given by the equation:
\(m=\rho V={4\over 3} \rho \pi r^3\)
A graph of \(m\) vs \(r\) will be a cubic function of general form:
\(y = Ax^3\)
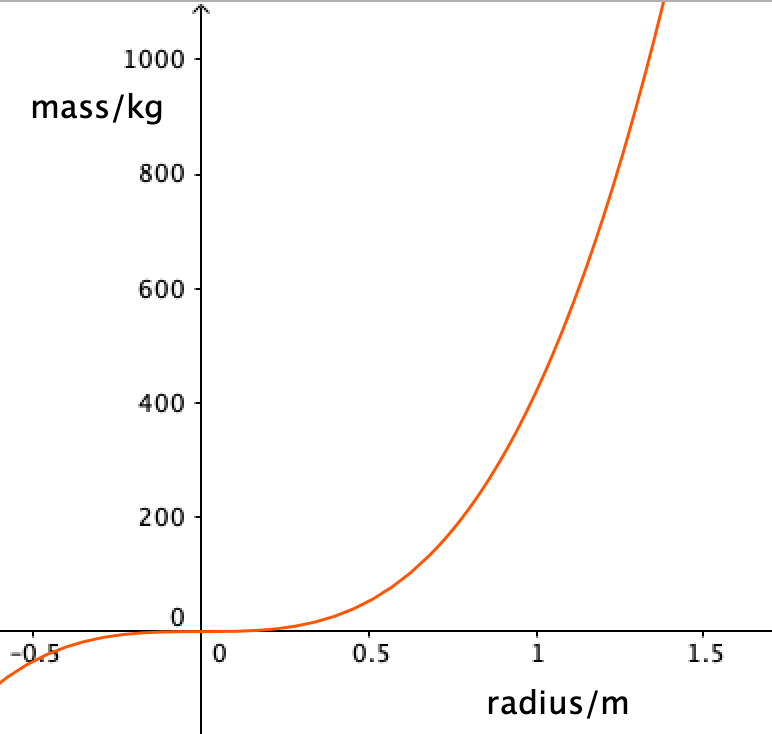
The equation of this line is \(y = 419x^3 \) so we can infer that \({4\over 3} ρπ = 419\). Therefore, density \(ρ = 1000\text{ kg m}^{-3}\).
Alternatively a straight line could be achieved by plotting mass against radius3:

This line has the equation \(y = Ax\), where \(A\) is the gradient. Comparing this with the equation for the sphere \(m = {4\over3} ρπr^3 \) we can conclude that \(A = {4\over 3} ρπ = 419\) and \(ρ = 1000\text{ kg m}^{-3}\).
Error bars
Error bars are lines drawn on the data points to indicate the size of the uncertainty. Vertical error bars are based on the uncertainty in the vertical axis measurements, and the same is true for horizontal error bars with the horizontal axis.
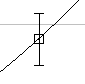
They give a visual representation of the uncertainty helping the experimenter to evaluate the validity of the data and the best fit line.
Here, the size of the error bars reflects the spread of data:

In this example, the error bars are too large in comparison with the spread of data. This is often the case when the 'half the range' method is used to estimate the uncertainty for multiple repeats:

In the next graph, the data and size of the error bars look reasonable, but there appears to be a systematic error. Either all \(x\) values are too small or all \(y\) values are too big. There is also an outlier. To find the cause of this anomaly, the original table of raw data can be revisited:
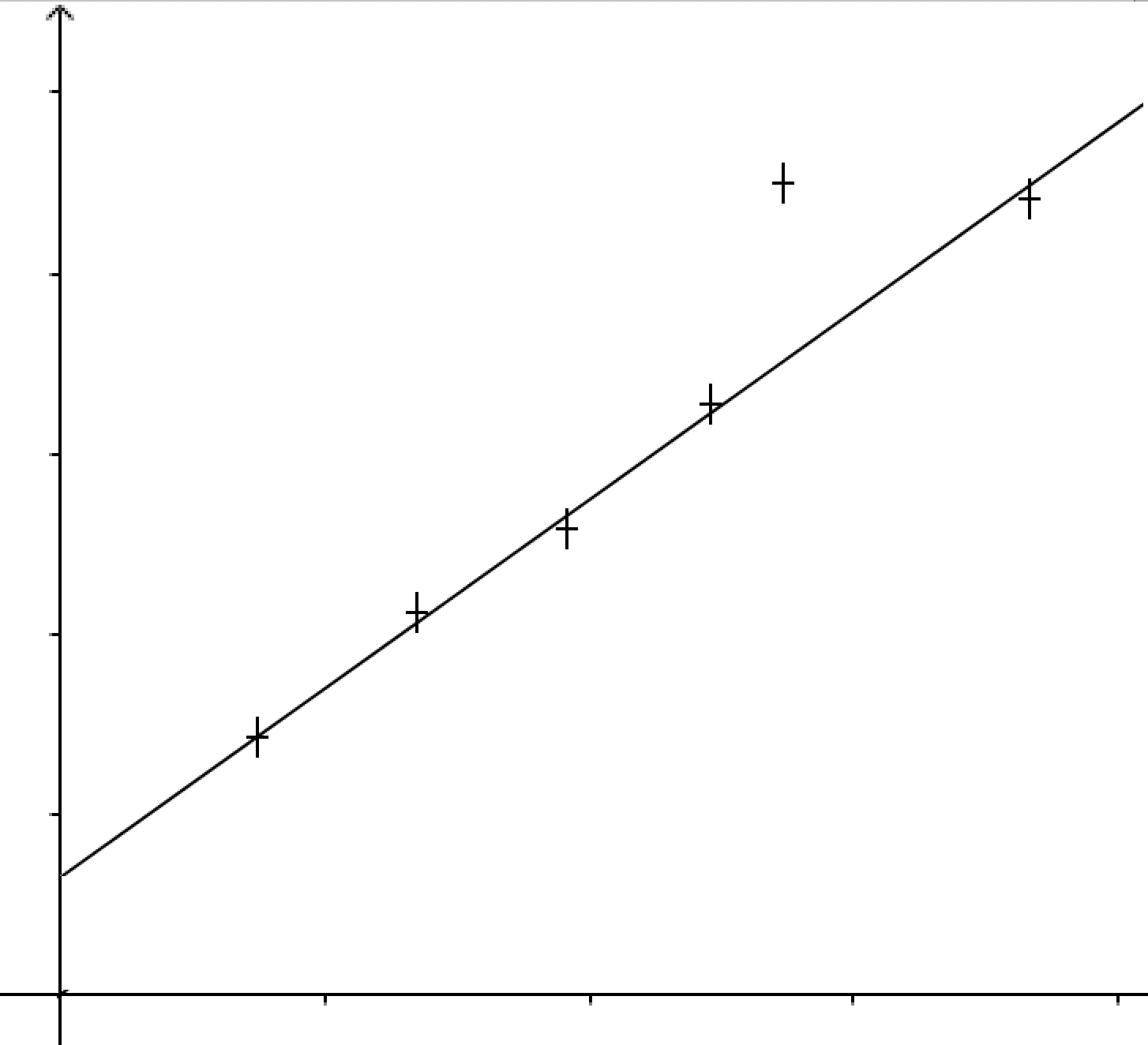
This best fit line does fit within the error bars but there appears to be a non-linear trend. This student should think again about what function they expected and what real-world factors may have breached their assumptions:

Uncertainty in gradient
The gradient of the best fit line will almost always give some known value e.g. the density. This value should be quoted with its uncertainty. To find the uncertainty in the gradient, the steepest and least steep lines of fit are plotted. These lines should touch all the error bars:

In some cases where it is difficult to estimate the size of error bars (e.g. an exponential relationship that has been linearised), these steepest and least steep lines of fit can be drawn by eye based on the spread of the data.
The graph below shows data collected with the mass of boxes estimated by comparing the boxes with a set of kg masses. This resulted in a rather large random error in the mass.
By moving the line using the blue dots estimate the max value for the mass of an apple.
The maximum gradient is 0.25 so the mass of an apple is 0.25 kg

