Activity: Intro to thermodynamics

This activity introduces the energy changes associated with gas transformations. You will state the first law of thermodynamics in terms of heat, internal energy and work, then use it to predict energy changes for different gas transformations. There are also some important terms to define (and become able to sketch on pV graphs): isochoric, isobaric, isothermal and adiabatic.
In this section we are going to look at the laws that model the energy flow in a thermodynamic system. The system considered will be a fixed mass of gas trapped in a cylinder by a piston but the laws apply to all thermodynamic systems.
An ideal gas is made of a large number of perfectly elastic spheres moving in random motion. There are no forces between the particles unless they collide.
- If you were to change the position of a gas atom would it require work to be done?

- Why don't we consider the PE of gas atoms?
We already know that:
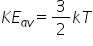
A mole contains NA atoms
- Write an expression for the internal energy of 1 mole of gas.
The universal gas constant, R = kNA
- Write an expression for U in terms of R and show that for n moles
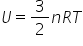
The PV diagram is a very useful tool for helping to apply the second law. Remember that although there are only 2 axis (P and V) T is also represented by the set of isothermals that cover the space. In this example (for 1.203 x 10-3 moles of course) we can see the isothermals for every 1000 K. They are not normally drawn but they are there.
In this example (for 1.203 x 10-3 moles of course) we can see the isothermals for every 1000 K. They are not normally drawn but they are there.
Determine whether the temperature will increase or decrease in the following cases:
- a gas expands from 100 cm3 to 300 cm3 at constant pressure
- a gas changes from a pressure of 200 kPa and volume 50 cm3 to a pressure of 400 kPa and a volume of 100 cm3.
From the graph we can deduce
If temperature increases ⇨ Increase in internal energy (+ΔU)
If volume gets bigger ⇨ Work done by gas (+W)
We can now apply this to some specific examples
To get a better understanding of the way the pV graph represents these changes you can build your own models in GeoGebra.
Thermodynamics simulation (GeoGebra)

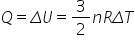
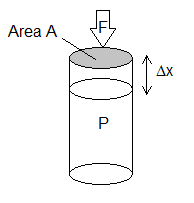 in this example the pressure is constant which means the force, F on the piston is also constant. This means that work done is simply F x distance moved by the piston = FΔx
in this example the pressure is constant which means the force, F on the piston is also constant. This means that work done is simply F x distance moved by the piston = FΔx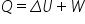
 Use the graph to determine
Use the graph to determine Use the graph to determine
Use the graph to determine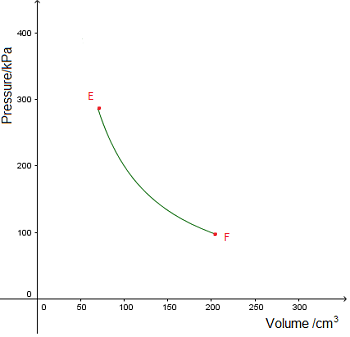 Use the graph to determine
Use the graph to determine Expansion (G → H)
Expansion (G → H)